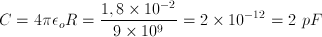Fisika Study Center

physics.fisikastudycenter.com-Learning capacitor in problems and solutions tutorial method. Finding equivalent capacitor in series and parallel combination, energy stored, potential difference across capacitors, electric charge storage, spherical capacitor and parallel plate-capacitors capacitance will be discussed.

Problem 1
Given a circuit contents a combination of three capacitors X, Y and Z , see the figure below.



If the switch S is ON, find:
a) circuit equivalent capacitance (equivalent capacitor)
b) electric charge stored in the circuit
c) electric charge stored in capacitor Z, use series principle
d) potential difference across capacitor Z
e) potential difference across capacitor X
f) potential difference across capacitor Y
g) electric charge stored in capacitor X
h) electric charge stored in capacitor Y
i) electric charge stored in capacitor Z
j) energy stored in the circuit
k) energy stored in capacitor X
l) energy stored in capacitor Y
m) energy stored in capacitor Z

Discussion
a) First replace X and Y parallel combination by its equivalent capacitance, named C_xy :



Replacing the two capacitors gives us the equivalent circuit in series combination, then find the equivalent for C_xy and C_z , the two are in series, called C_eq or C_tot :



b) Charge stored in the circuit or the charge in the equivalent capacitance; Q_tot , C_tot multipled by V_tot



c) Charge stored in capacitor Z; Q_z

For series combination, the charge is the same on all capacitors, it's the same as the charge on the equivalent capacitor :



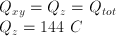
d) potential difference across capacitor Z; named V_z



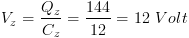
e) potential difference across capacitors X and Z are the same cause of parallel combination



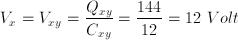
f) potential difference across Y is the same as potential difference across X



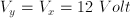
g) charge in capacitor X, be careful, it's not the same as charge in equivalent capacitor



h) charge in capacitor Y



i) charge in capacitor Z



j) energy stored in the circuit
Use one of these three formula to get the energy stored



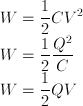
So then



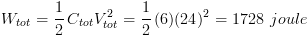
k) energy stored in capacitor X



l) energy stored in capacitor Y



m) energy stored in capacitor Z



Problem 2
Given three capacitor in a circuit below, the voltage source is 24 volt.



If the switch is ON, find :
a) circuit equivalent capacitancy
b) electric charge stored in circuit
c) electric charge stored in capacitor Z
d) potential difference across capacitor Z
e) potential difference across capacitor X
f) potential difference across capacitor Y
g) electric charge stored in capacitor X
h) electric charge stored in capacitor Y
i) energy stored in the circuit
j) energy stored in capacitor X
k) energy stored in capacitor Y
l) energy stored in capacitor Z

Try ..!!

Problem 3
Given a parallel-plate capacitor in vacuum. The plates of capacitor are 2 cm apart and 50 cm² in area of each plate. A potrntial difference of 120 volt is applied acroos capacitor. When ε_o is 8,85 x 10^{− 12} C² N ^{− 1 − 2} calculate :
a) capacitor capacitane
b) charge stored in capacitor
c) the magnitude of electric charge in space between the two plates of capacitor

Answer
a) capacitor capacitance



b) charge stored in capacitor



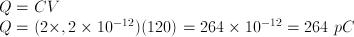
c) the magnitude of electric charge in space between the two plates of capacitor



Problem 4
A plate-capacitor of capacitance C in vacuum. If then a material with its dielectric constant K = 2 is inserted between capacitor plates, find the new capacitance of capacitor!

Answer
There are no changing in area and plates separation distance of capacitor, so then the new capacitance is



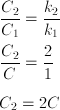
Problem 5
Given a parallel plate-capacitor of 1200 μF in vacuum. If the area of capacitor plates are doubled and the separation between two plates is 1.5 times the original, find the new capacitance of the capacitor!

Answer



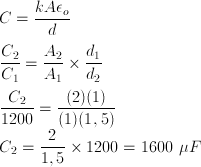
Problem 6
A spherical capacitor with its radius of 1.8 cm. When 1/4πε_o = 9 x 10⁹ in international unit, find the capacitance of this spherical capacitor!

Answer
The capacitance of spherical capacitor with radius of R :