5 Common Problems of Fluid Dynamics
- Category: High School
- Written by fisikastudycenter
physics.fisikastudycenter.com- learning fluid dynamics and bernoulli's equation in 5 common problems of fluid dynamics includes volume flow of rate, continuity equation and bernoulli's and torricelli's equation. Prepared for grade 11 high school level.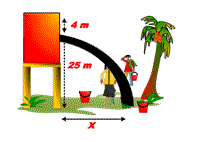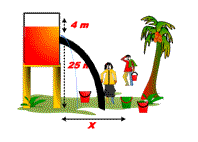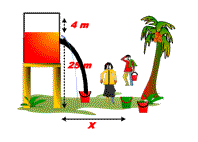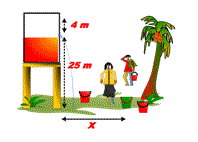
Formulas
Volume of flow rate
Q = V/t
Q = Av
where:
Q = volume of flow rate (m3/s)
V = volume (m3)
t = time (s)
A = area (m2)
v = speed of flow (m/s)
1 liter = 1 dm3 = 10−3 m3
Continuity equation
Q1 = Q2
A1v1 = A2v2
Bernoull's Equation
P + 1/2 ρv2 + ρgh = Constant
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
where :
P = pressure (Pascal = Pa = N/m2)
ρ = fluid density (kg/m3)
g = acceleration due to gravity (m/s2)
Fluid tank with a hole
v = √(2gh)
X = 2√(hH)
t = √(2H/g)
where :
v = speed of fluid flow from the hole
X = horizontal distance reached by the fluid flow at first time
h = the distance of fluid surface to the hole
H = distance between the point of fluid drop to the hole
t = time taken by the fluid to reach the drop point
Question 1
Ahmad fills a bucket of 20 liter of capacity through opening a water channel. 
If the area of channel with diameter of r D2 is 2 cm2 and the water flow speed in the channel is 10 m/s find:
a) water volume rate
b) time taken to make the bucket full of water
Answer
Data :
A2 = 2 cm2 = 2 x 10−4 m2
v2 = 10 m/s
a) water volume rate
Q = A2v2 = (2 x 10−4)(10)
Q = 2 x 10−3 m3/s
b) time taken to full the bucket
Data :
V = 20 liter = 20 x 10−3 m3
Q = 2 x 10−3 m3/s
t = V / Q
t = ( 20 x 10−3 m3)/(2 x 10−3 m3/s )
t = 10 sec
Question 2
An underground water channel is shown in the figure below! 
If the area of wider channel is 5 m2 , the little one is 2 m2 and the sped of water flow in wide channel is 15 m/s, find the speed of water flow in A2 area!
Answer
Using continuity equation
A1v1 = A2v2
(5)(15) = (2) v2
v2 = 37,5 m/s
Question 3
A water tank with a little hole in its side shown below! 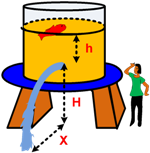
The location of hole from the ground is at distance H = 10 m and the distance of the hole to the water surface is h = 3,2 m. Find:
a) speed of water flow from the hole
b) distance x reached by water flow
c) time taken by the water flow to reach the ground at the first time
Answer
a) speed of water flow
v = √(2gh)
v = √(2 x 10 x 3,2) = 8 m/s
b) distance x reached by water flow
X = 2√(hH)
X = 2√(3,2 x 10) = 8√2 m
c) time taken by the water flow to reach the ground at the first
t = √(2H/g)
t = √(2(10)/(10)) = √2 sec
Question 4
A ventury meter, used to measured speed flow in a pipe is shown below below! 
The areas of the wide part and the narrow part of pipe are 5 cm2 and 3 cm2 respectively. The difference in height between the two vertical tubes is 20 cm, find :
a) speed flow at the wide part
b) sped flow at narrow part
Answer
a) speed flow at the wide part
v1 = A2√ [(2gh) : (A12 − A22) ]
v1 = (3) √ [ (2 x 10 x 0,2) : (52 − 32) ]
v1 = 3 √ [ (4) : (16) ]
v1 = 1,5 m/s
Calculation Tips :
Keep the unit of areas in cm2 , g and h are in m/s2 and m. then v will be in m/s.
b) sped flow at narrow part
A1v1 = A2v2
(3 / 2)(5) = (v2)(3)
v2 = 2,5 m/s
Question 5
The water installation using pipes at a home shown below! The ratio of wide area and narrow area is 4 : 1. 
h1 is 5 m from the floor and h2 is 1 m diatas tanah. The water flow speed at wider area A1 is 36 km/hour with the pressure of 9,1 x 105 Pa. Find :
a) water flow speed at the narrow pipe
b) the pressure difference between two pipes
c) pressure at the narrow pipe
Use the water density (ρair = 1000 kg/m3)
Answer
Data :
h1 = 5 m
h2 = 1 m
v1 = 36 km/jam = 10 m/s
P1 = 9,1 x 105 Pa
A1 : A2 = 4 : 1
a) water flow speed at the narrow pipe
From continuity equation :
A1v1 = A2v2
(4)(10) = (1) (v2)
v2 = 40 m/s
b) the pressure difference between two pipes
From Bernoull's equation:
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) + ρg(h2 − h1)
P1 − P2 = 1/2(1000)(402 − 102) + (1000)(10)(1 − 5)
P1 − P2 = (500)(1500) − 40000 = 750000 − 40000
P1 − P2 = 710000 Pa = 7,1 x 105 Pa
c) pressure at the narrow pipe
P1 − P2 = 7,1 x 105
9,1 x 105 − P2 = 7,1 x 105
P2 = 2,0 x 105 Pa