Fisika Study Center

Fisikastudycenter.com- The Examples of High School Physics Problems and Solutions for Grade 10, Motion along Straight Line : Constant Velocity, Uniform Accelerated Motion.


Problem 1
A stone of 200 g throw up with 50 m/sec of initial velocity.



Ignore the air friction and use the acceleration due to gravity g = 10 m/sec², find :
a) The maximum height of stone
b) Time taken to reach the maximum height
c) Time taken by the stone before reaching the ground.

Solution
a) The stone velocity = 0 m/sec, in it's maximum height. Using accelerated motion formula:



b) The time taken:



c) Time for the stone in the air:

t = (2)(5) = 10 sec

Problem 2
A car moves at speed of 72 km/hrs, before the breaks works and finally stops at 8 m after the break works. Find the acceleration of the car!

Solution
First, convert the unit of speed from km/hrs to m/sec.Using the formula:

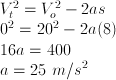
Problem 3
Given a graph shown below:



Find:
a. distance for t = 5 sec till t = 10 sec
b. the displacement for t = 5 sec till t = 10 sec

Solution
Finding the distance when given a graph of V (speed) - t (time) : Calculate the area of V-t graph (under the lines till t axis), all area is positif value, for calculating the distance, above the t axis also under t axis. For calculating the distance, use the same methode, but the above t axis area is positif, under the t axis is negative value,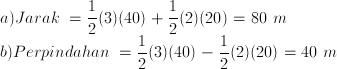



Problem 4
An ant moves from point A to point B as shown below.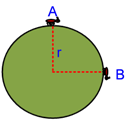



The radius of circle is r = 2m, and the ant need 10 sec to reach point B.Find:
a) The average velocity
b) The average speed

Solution
We have to calculate the distance and displacement of the ant first:

Distance = ¹/₄ (2πr) = ¹/₄ (2π x 2) = π m

Displacement, use phytagorean:
Displacement = √ ( 2² + 2² ) = 2√2 meter.

a) Average velocity = displacement : time
Average velocity = 2√2 meter : 10 sec = 0,2√2 m/sec

b) Average speed = distance : time
Average speed = π meter : 10 sec = 0,1 π m/sec

Problem 5
An airplane moves from P to Q at the east direction for 30 minutes with constant velocity of 200 km/hrs. From Q the plane moves to R that located 53^o from east direction an need 1 hr flaying with constant average of 100 km/hr.



Find:
a) The average velocity of the plane
b) The average speed of the plane

Solution
First, find the length of PQ, QR, QR', RR', PR' and PR



PQ = V_PQ x t_PQ = (200 km/jam) x (0,5) jam = 100 km
QR = V_QR x t_QR = (100 km/jam) x (1 jam) = 100 km
QR' = QR cos 53^o = (100 km) x (0,6) = 60 km
RR' = QR sin 53^o = (100 km) x (0,8) = 80 km
PR' = PQ + QR' = 100 + 60 = 160 km

PR = √[ (PR' )² + (RR')² ]
PR = √[ (160 )² + (80)² ] = √(32000) = 80√5 km

the distance = PQ + QR = 100 +100 = 200 km
the displacement = PR = 80√5 km
the time taken = 1 hr + 0,5 hr = 1,5 hrs

a) The average velocity = displacement : time taken = 80√5 km : 1,5 hr = 53,3 √5 km/hr
b) average speed = distance : time taken = 200 km : 1,5 hr = 133,3 km/hr